

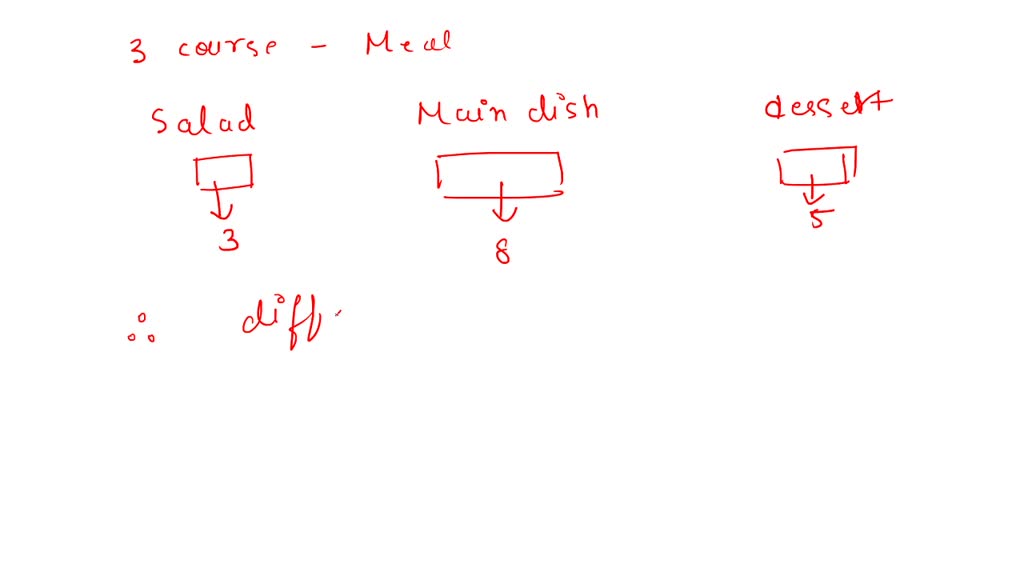
Sandwiches: Chicken Salad, Turkey, Grilled Cheeseĭraw a tree diagram to find the total number of possible outcomes.With the combo meal, you get 1 sandwich, 1 side, and 1 drink. Look at the tree diagram for this problem:Ī new restaurant has opened, and they offer lunch combos for $5.00. However, this can be applied to an infinite number of choices or possibilities, which opens the door for some neat shortcuts. If there are m ways to choose a first item, and n ways to choose a second item, after the first item has been chosen, then there are m*n ways to choose both items.The idea of combinations and permutations offers an opportunity to skip the tree diagram and still get the correct answer without spending hours drawing lines and making sure you haven't skipped an outcome.īefore we can discuss combinations and permutations, we must first understand the idea of the Fundamental Counting Principle (FCP), that states: However, there are usually way too many possibilities, making a tree diagram impractical. Sometimes, when we are talking about the idea of probability, it is possible to create a tree diagram that has all possible outcomes.
#Math counting principle series#
For how many years could this policy be continued before exactly the same program would have to be repeated?Īny ideas would be helpful to recognize the clues in the problems.So far in this Probability: An Overview series of Related Lessons, found in the right-hand sidebar, you have studied experimental and theoretical probability as well as dependency. The composer Beethoven wrote 9 symphonies, 5 piano concertos (music for piano and orchestra), and 32 piano sonatas (music for solo piano).Ī) How many ways are there to play first a Beethoven symphony and then a Beethoven piano concerto?ī) The manager of a radio station decides that on each successive evening (7 days per week), a Beethoven symphony will be played followed by a Beethoven piano concerto followed by a Beethoven piano sonata. If 6 bottles are randomly selected, what is the probability that all of them are the same variety? If 6 bottles are randomly selected, what is the probability that this results in two bottles of each variety being chosen? If 6 bottles are randomly selected, how many ways are there to obtain two bottles of each variety? If 6 bottles of wine are to be randomly selected from the 30 for serving, how many ways are there to do this?

If he wants to serve 3 bottles of zinfandel and serving order is important, how many ways are there to do this? His current wine supply includes 8 bottles of zinfandel, 10 of merlot, and 12 of cabernet (he only drinks red wine), all from different wineries. Here's one that uses the permutations / combinations according to my student solutions manualĪ friend of mine is giving a dinner party. I have 2 example problems and what would help the most is key things to look to recognize using the counting principle vs permutations / combinations formulas. Currently, I'm stuck on recognizing key points in a problem involving permutations / combinations vs. It covers Probability extensively and other stats topics. I've been studying stats, and currently taking my first ever engineering based stats course in college.


 0 kommentar(er)
0 kommentar(er)
